Geometry iep goals 10th grade – Embark on an enlightening journey through Geometry IEP Goals for 10th Grade, where the intricacies of geometric concepts unfold in a captivating narrative. This comprehensive guide delves into the fundamental principles and theorems that shape the world of geometry, empowering learners with the knowledge and skills to conquer geometric challenges with confidence.

Throughout this exploration, we will unravel the properties and relationships between geometric shapes, unravel the mysteries of transformations and symmetry, and uncover the practical applications of trigonometry. Prepare to engage in logical reasoning and problem-solving, harnessing the power of technology to enhance your understanding of geometry.

Geometry IEP Goals for 10th Grade

Geometry in 10th grade focuses on developing students’ understanding of advanced geometric concepts and their applications. These concepts lay the foundation for higher-level mathematics and real-world problem-solving.

Essential Concepts

Essential geometry concepts covered in 10th grade include:

• Shapes and their properties:Classifying polygons, triangles, circles, and other shapes based on their properties such as number of sides, angles, and symmetry.
• Angles and their relationships:Understanding different types of angles, their measurements, and their relationships in various geometric figures.
• Similarity and congruence:Determining whether two shapes are similar or congruent based on their properties and transformations.
• Coordinate geometry:Using the coordinate plane to locate points, plot graphs, and solve geometric problems.
• Trigonometry:Introducing basic trigonometric ratios (sine, cosine, tangent) and their applications in solving real-world problems.

Understanding Geometric Properties and Relationships

Geometry involves studying the properties and relationships between various geometric shapes, such as triangles, circles, and quadrilaterals. Understanding these properties is crucial for solving geometry problems and applying geometric concepts in real-world situations.

Geometric Shapes and Their Properties

Geometric shapes have specific properties that define their characteristics. For example, triangles have three sides and three angles, and their sum of interior angles is always 180 degrees. Circles are defined by their radii and circumferences, and their areas are calculated using the formula πr².

Quadrilaterals, such as squares, rectangles, and trapezoids, have four sides and their properties vary based on their specific types.

Geometric Formulas

Geometric formulas are mathematical equations used to calculate measurements related to geometric shapes. These formulas allow us to determine the area, perimeter, and volume of various shapes. For example, the area of a triangle is calculated using the formula (1/2)

• base
• height, while the volume of a rectangular prism is calculated using the formula length
• width
• height. Understanding and applying these formulas is essential for solving geometry problems and making accurate calculations.

Transformations and Symmetry

Transformations are operations that move or change the position of a geometric figure without changing its size or shape. There are three main types of transformations: translations, rotations, and reflections.

Geometry IEP goals for 10th grade often include developing spatial reasoning skills. These skills can be applied to real-world situations, such as understanding the impact of a natural disaster like a hurricane. For example, students can learn about the impact of Hurricane Harvey on Texas and use their geometry skills to analyze the damage and design solutions for rebuilding.

By connecting geometry to real-world events, students can see the practical applications of their learning and develop a deeper understanding of the subject.

Translations

• A translation moves a figure from one point to another without changing its orientation.
• Translations are described by a vector, which has both a magnitude and a direction.
• The magnitude of the vector represents the distance the figure is moved, and the direction of the vector represents the direction in which the figure is moved.

Rotations

• A rotation turns a figure around a fixed point called the center of rotation.
• Rotations are described by an angle of rotation, which is measured in degrees.
• The angle of rotation represents the amount the figure is turned.

Reflections

• A reflection flips a figure over a line called the line of reflection.
• Reflections are described by the line of reflection.
• The line of reflection is the line that the figure is flipped over.

Symmetry is a property of a figure that has two or more parts that are mirror images of each other. There are two main types of symmetry: line symmetry and rotational symmetry.

Line Symmetry

• A figure has line symmetry if it can be divided into two congruent halves by a line.
• The line that divides the figure into two congruent halves is called the line of symmetry.

Rotational Symmetry

• A figure has rotational symmetry if it can be rotated around a point by a certain angle and look exactly the same.
• The point around which the figure is rotated is called the center of rotation.
• The angle by which the figure is rotated is called the angle of rotation.

Transformations and symmetry are important concepts in geometry. They can be used to solve a variety of geometric problems, such as finding the area and perimeter of a figure, and determining the volume of a solid.

Trigonometry and Applications

Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It has many applications in real-world problems, such as navigation, surveying, and architecture.Trigonometry is based on the idea of trigonometric ratios. The sine, cosine, and tangent of an angle are ratios of the sides of a right triangle that contains the angle.

These ratios can be used to find the missing sides or angles of a triangle.

Solving Real-World Problems

Trigonometry can be used to solve a variety of real-world problems. For example, it can be used to:* Find the height of a building or tree

• Determine the distance to a star
• Calculate the angle of a projectile
• Design a bridge or other structure

Trigonometry is a powerful tool that can be used to solve a wide variety of problems. It is an essential part of many fields, including mathematics, science, and engineering.

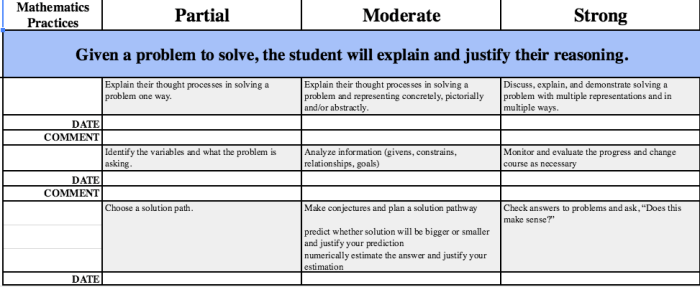
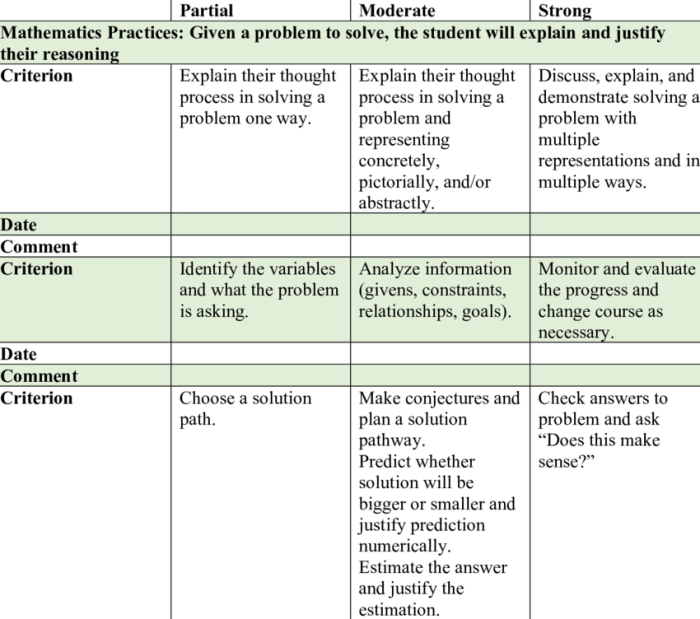
Geometric Reasoning and Problem-Solving

Geometric reasoning and problem-solving are essential skills for success in geometry and beyond. Logical thinking and the ability to apply geometric principles are crucial for understanding complex concepts and solving real-world problems.

Deductive reasoning is a fundamental tool in geometry. By using axioms, postulates, and previously proven theorems, students can derive new conclusions and solve problems. Proof is a formal way of demonstrating the validity of a statement using deductive reasoning.

Strategies for Solving Geometric Problems

• Understand the problem: Read the problem carefully and identify the given information and what is being asked.
• Draw a diagram: Sketching a diagram can help visualize the problem and identify relevant relationships.
• Apply geometric principles: Use theorems, postulates, and definitions to establish relationships between the elements of the diagram.
• Use logical reasoning: Apply deductive reasoning to derive new conclusions and solve the problem.
• Check your answer: Verify that the solution satisfies the given conditions and makes sense in the context of the problem.

Real-World Applications, Geometry iep goals 10th grade

• Architecture: Designing buildings and structures requires an understanding of geometric principles to ensure stability and aesthetics.
• Engineering: Engineers use geometry to design bridges, machines, and other structures that withstand forces and meet specific requirements.
• Surveying: Surveyors use geometry to measure and map land areas, determine property boundaries, and plan construction projects.

li>Computer graphics: Geometric concepts are used in computer graphics to create 3D models, animations, and virtual environments.

Technology Integration in Geometry: Geometry Iep Goals 10th Grade

Technology plays a crucial role in enhancing geometry education by providing powerful tools for visualization, problem-solving, and accessibility.

Geometric software like GeoGebra and Sketchpad enable students to construct and manipulate geometric figures, explore dynamic relationships, and visualize complex concepts in an interactive environment. These tools foster spatial reasoning, problem-solving skills, and the ability to make connections between geometric properties and their applications.

Online Resources for Visualization and Problem-Solving

Online resources such as Khan Academy, Desmos, and Wolfram Alpha offer interactive simulations, videos, and tutorials that support students in understanding geometric concepts and solving problems.

• Khan Academy provides comprehensive video lessons and exercises that cover a wide range of geometry topics.
• Desmos offers a free online graphing calculator that allows students to plot geometric figures, explore transformations, and analyze relationships.
• Wolfram Alpha provides a powerful computational knowledge engine that can generate step-by-step solutions to geometry problems.

Technology for Diverse Learning Needs

Technology can support students with diverse learning needs by providing:

• Visual aids and interactive simulations that cater to students with visual or spatial learning preferences.
• Assistive technology tools, such as screen readers and speech-to-text software, that enable students with disabilities to access and engage with geometry content.
• Differentiated instruction and personalized learning pathways that allow students to progress at their own pace and focus on areas where they need additional support.

Assessment and Evaluation of Geometry Skills

Assessing geometry skills in 10th grade is crucial for monitoring student progress and ensuring they grasp the concepts thoroughly. This involves employing various assessment methods that cater to different learning styles and skill levels.

Formative and summative assessments play significant roles in the assessment process. Formative assessments provide ongoing feedback during the learning process, allowing teachers to identify areas where students need additional support. Summative assessments, on the other hand, evaluate students’ overall understanding of the geometry concepts covered in a unit or course.

Creating Effective Geometry Assessments

Creating effective geometry assessments requires careful planning and consideration. Here are some guidelines to ensure assessments are valid, reliable, and provide meaningful information about student learning:

• Align assessments with learning objectives:Assessments should directly measure the specific geometry skills and concepts that have been taught.
• Use a variety of assessment methods:Incorporate different assessment methods such as quizzes, tests, projects, presentations, and portfolios to cater to diverse learning styles.
• Provide clear instructions and rubrics:Ensure students understand the assessment requirements and expectations by providing clear instructions and rubrics.
• Incorporate open-ended questions:Open-ended questions allow students to demonstrate their understanding of geometry concepts in their own words and provide insights into their thought processes.
• Use technology for assessment:Technology can enhance assessment by providing interactive and engaging activities, simulations, and online quizzes.

Differentiated for Geometry

Differentiated in geometry involves adapting lessons to meet the diverse learning needs of students. It ensures that all learners can access and engage with the content effectively.

To differentiate geometry lessons, teachers can use various strategies, such as:

Adapting Content

• Provide materials at different reading levels.
• Offer alternative representations of concepts (e.g., visual aids, manipulatives).
• Adjust the depth and complexity of tasks.

Adapting Process

• Allow students to choose from a variety of learning activities.
• Provide scaffolding and support for struggling students.
• Challenge advanced students with enrichment activities.

Adapting Product

• Offer students multiple options for demonstrating their learning (e.g., presentations, projects, essays).
• Set different expectations for different students.
• Provide feedback that is specific and tailored to individual needs.

Examples of differentiated activities and resources for geometry include:

• Tiered assignments with varying levels of difficulty.
• Choice boards that allow students to select activities based on their interests and strengths.
• Manipulatives and hands-on activities for kinesthetic learners.
• Online simulations and virtual manipulatives.
• Technology tools that provide scaffolding and support (e.g., interactive geometry software).

Question Bank

What are the core concepts covered in Geometry IEP Goals for 10th Grade?

The core concepts include understanding geometric shapes, angles, and measurements; exploring properties and relationships between shapes; applying geometric formulas; investigating transformations and symmetry; utilizing trigonometry to solve real-world problems; and developing logical reasoning and problem-solving skills.

How can technology enhance geometry learning?

Technology offers interactive visualization tools, geometric software, and online resources that support diverse learning needs. It enables students to explore concepts visually, manipulate shapes dynamically, and solve complex problems efficiently.

What is the importance of differentiated instruction in geometry?

Differentiated instruction recognizes that learners have unique strengths and needs. By adapting lessons and activities, teachers can provide targeted support and challenge to each student, ensuring that all learners have opportunities to succeed.