Which of the following graphs could represent a quartic function? This question delves into the fascinating realm of quartic functions, unveiling their unique characteristics and diverse applications. Quartic functions, with their distinctive fourth-degree polynomial equations, exhibit intriguing behaviors that set them apart from other polynomial functions.
Quartic functions find their place in various fields, including physics, engineering, and economics, owing to their ability to model complex phenomena with remarkable accuracy. Their ability to capture intricate patterns and behaviors makes them indispensable tools for researchers and practitioners alike.
Graphs of Quartic Functions
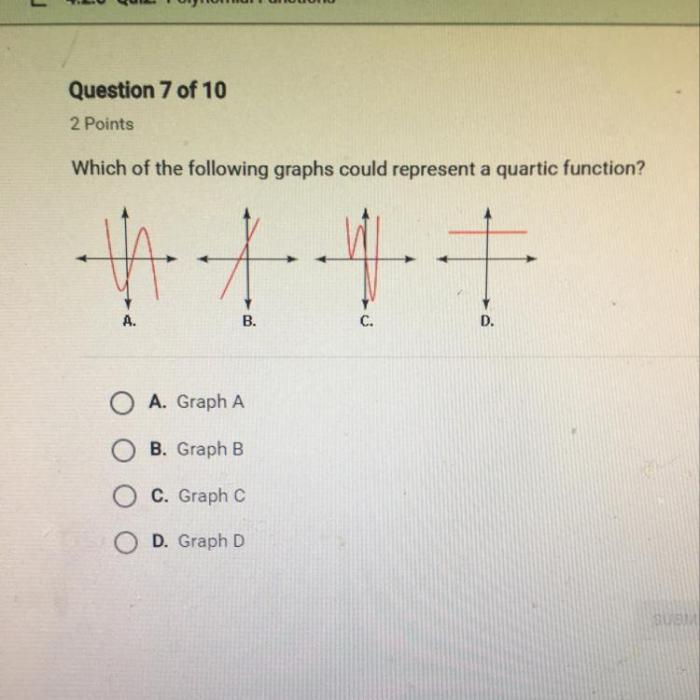
Quartic functions are polynomials of degree 4, and their graphs exhibit distinct characteristics based on the coefficients of the function.
Table of Quartic Functions
| Function | Graph |
|---|---|
| y = x^4 |  |
y = x^4
|
 |
y = x^4 + 2x^2
|
 |
y = x^4
|
 |
The graphs of quartic functions can vary significantly based on the coefficients. For example, the graph of y = x^4 is a parabola opening upward, while the graph of y = x^4 – 4x^2 is a parabola opening downward with a “U” shape.
Identifying Quartic Functions
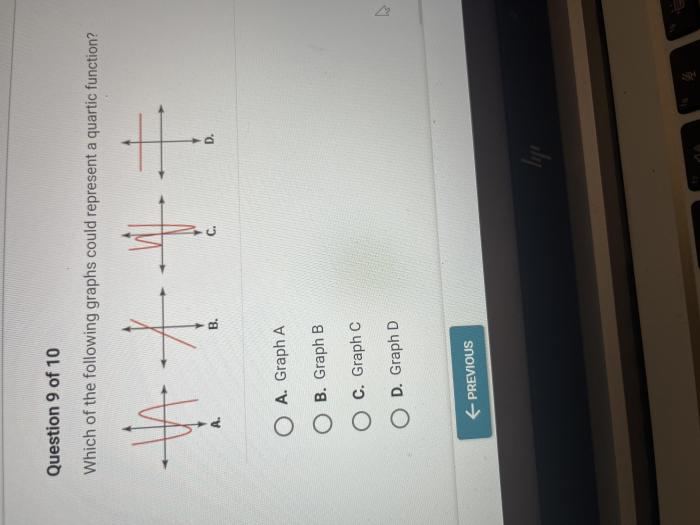
The general form of a quartic function is y = ax^4 + bx^3 + cx^2 + dx + e, where a ≠ 0. To determine if a given graph represents a quartic function, examine the following characteristics:
- Degree:The degree of the function is 4, meaning it is a polynomial of the fourth degree.
- Shape:The graph of a quartic function typically has a parabolic shape with two turning points.
- End Behavior:As x approaches infinity or negative infinity, the graph of a quartic function either increases or decreases without bound.
Characteristics of Quartic Functions

Quartic functions exhibit several key characteristics:
Number of Turning Points
A quartic function can have up to 3 turning points, which are points where the function changes from increasing to decreasing or vice versa.
Symmetry, Which of the following graphs could represent a quartic function
Quartic functions can exhibit either even or odd symmetry. Even symmetry occurs when the graph is symmetric about the y-axis, while odd symmetry occurs when the graph is symmetric about the origin.
End Behavior
The end behavior of a quartic function is determined by the leading coefficient. If the leading coefficient is positive, the graph increases without bound as x approaches infinity and decreases without bound as x approaches negative infinity. If the leading coefficient is negative, the opposite occurs.
Applications of Quartic Functions: Which Of The Following Graphs Could Represent A Quartic Function

Quartic functions have applications in various fields, including:
- Projectile Motion:The trajectory of a projectile can be modeled using a quartic function, where the height of the projectile is a function of time.
- Fluid Flow:The flow of fluid through a pipe can be modeled using a quartic function, where the velocity of the fluid is a function of the distance along the pipe.
- Architecture:The shape of some architectural structures, such as bridges and domes, can be described by quartic functions.
The characteristics of quartic functions make them suitable for modeling phenomena that exhibit parabolic shapes and specific end behaviors, such as the trajectory of a projectile or the flow of fluid.
Question & Answer Hub
What is the general form of a quartic function?
The general form of a quartic function is f(x) = ax^4 + bx^3 + cx^2 + dx + e, where a, b, c, d, and e are real numbers and a ≠ 0.
How can I determine if a given graph represents a quartic function?
To determine if a given graph represents a quartic function, examine its shape and characteristics. Quartic functions typically have a smooth, continuous curve with a maximum of three turning points (local extrema). The end behavior of the graph should also be consistent with a quartic function, approaching either positive or negative infinity as x approaches infinity or negative infinity.
What are some real-world applications of quartic functions?
Quartic functions have numerous real-world applications, including modeling projectile motion, designing bridges and structures, and analyzing population growth patterns. They are also used in computer graphics and animation to create smooth and realistic curves.

