Midpoint and distance in the coordinate plane assignment answer key – Delving into the intricacies of midpoint and distance calculations within the coordinate plane, this comprehensive answer key serves as an invaluable resource for students and educators alike. With its meticulously crafted explanations and detailed examples, this guide unlocks a deeper understanding of these fundamental geometric concepts.

The ensuing sections delve into the intricacies of the midpoint formula, providing a step-by-step approach to determining the midpoint of a line segment. The distance formula is also thoroughly examined, empowering readers to calculate the distance between any two points in the coordinate plane with precision.

Midpoint and Distance in the Coordinate Plane: Midpoint And Distance In The Coordinate Plane Assignment Answer Key

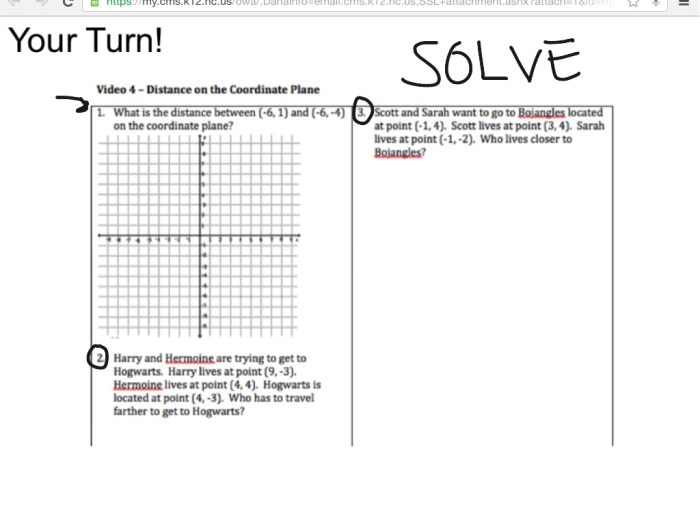
The midpoint and distance formulas are two important tools for solving geometry problems. The midpoint formula allows us to find the coordinates of the midpoint of a line segment, while the distance formula allows us to find the distance between two points.

Midpoint Formula

The midpoint formula is given by:

$$M=(\fracx_1+x_22, \fracy_1+y_22)$$

where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of the endpoints of the line segment.

Example:Find the midpoint of the line segment with endpoints $(2, 3)$ and $(4, 7)$.

Using the midpoint formula, we get:

$$M=(\frac2+42, \frac3+72)$$

$$M=(3, 5)$$

Distance Formula, Midpoint and distance in the coordinate plane assignment answer key

The distance formula is given by:

$$d=\sqrt(x_2-x_1)^2+(y_2-y_1)^2$$

where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of the two points.

Example:Find the distance between the points $(2, 3)$ and $(4, 7)$.

Using the distance formula, we get:

$$d=\sqrt(4-2)^2+(7-3)^2$$

$$d=\sqrt4+16$$

$$d=\sqrt20$$

$$d=2\sqrt5$$

Applications of Midpoint and Distance Formulas

The midpoint and distance formulas can be used to solve a variety of geometry problems. For example, they can be used to:

• Find the center of a circle
• Find the length of a line segment
• Determine whether two line segments are parallel or perpendicular

The midpoint and distance formulas are also used in a variety of real-world applications, such as:

• Navigation
• Engineering
• Architecture

Question & Answer Hub

What is the midpoint formula?

The midpoint formula is (x1 + x2) / 2, (y1 + y2) / 2, where (x1, y1) and (x2, y2) represent the coordinates of the endpoints of the line segment.

How do I use the distance formula?

The distance formula is sqrt((x2 – x1)^2 + (y2 – y1)^2), where (x1, y1) and (x2, y2) represent the coordinates of the two points.